学习《精通开关电源设计》第二章
目前未能完成hexo对latex的支持,博客公式部分会出现乱码
2.1 直流传递函数
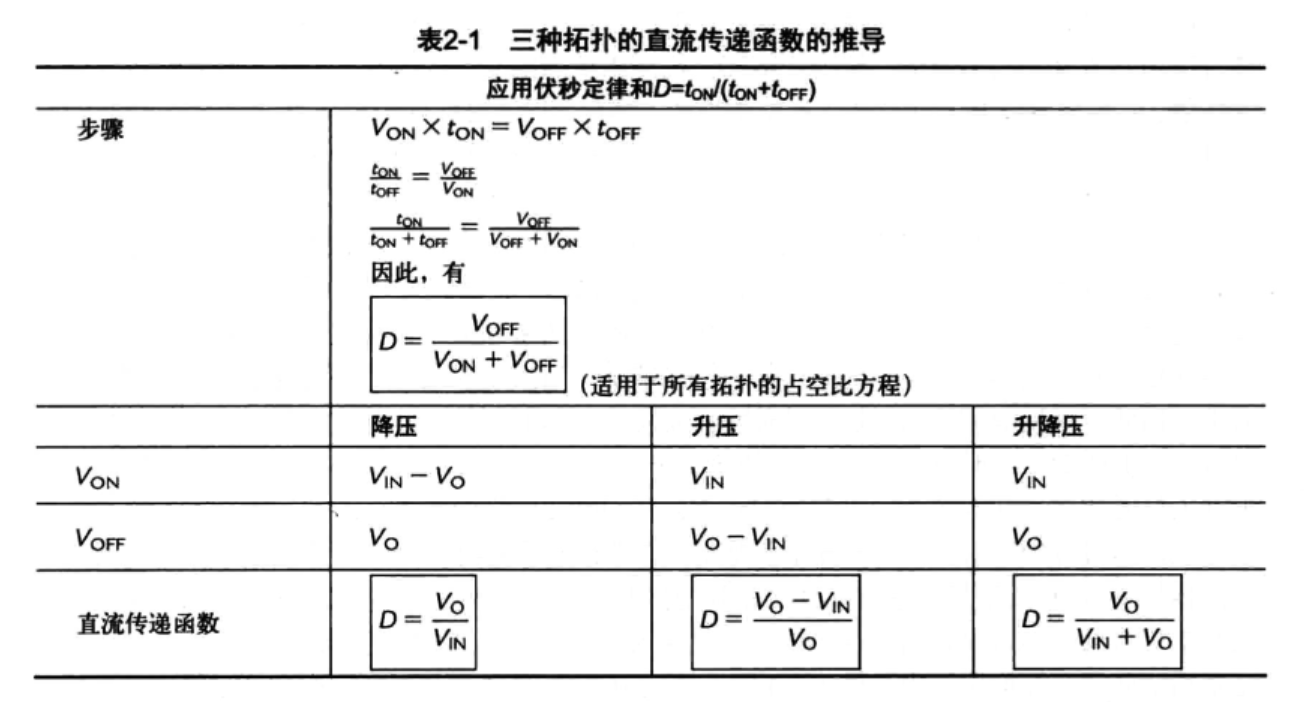
2.2 电感电流波形中的直流分量和交流分量

$$\Delta I=\frac{V_{\Delta t}}{L}=\frac{VDT}{L}=\frac{UD}{Lf}.$$
可以看出$\Delta I$与V、D、L、和f之间的关系
$$\begin{aligned}I_{DC}\equiv I_{0}&(\text{降压})\I_{DC}=\frac{I_{0}}{1-D}&(\text{升压、升降压}).\end{aligned}$$
可以看出电感直流电流大小与负载电流直接相关,升压、升降压拓扑中海域占空比大小有关
!!!
需要认识到,在升压、升降压拓扑中,当占空比接近1时,电感直流电流大小会以极大的斜率上升
2.3 交流电流、直流电流和峰值电流的定义
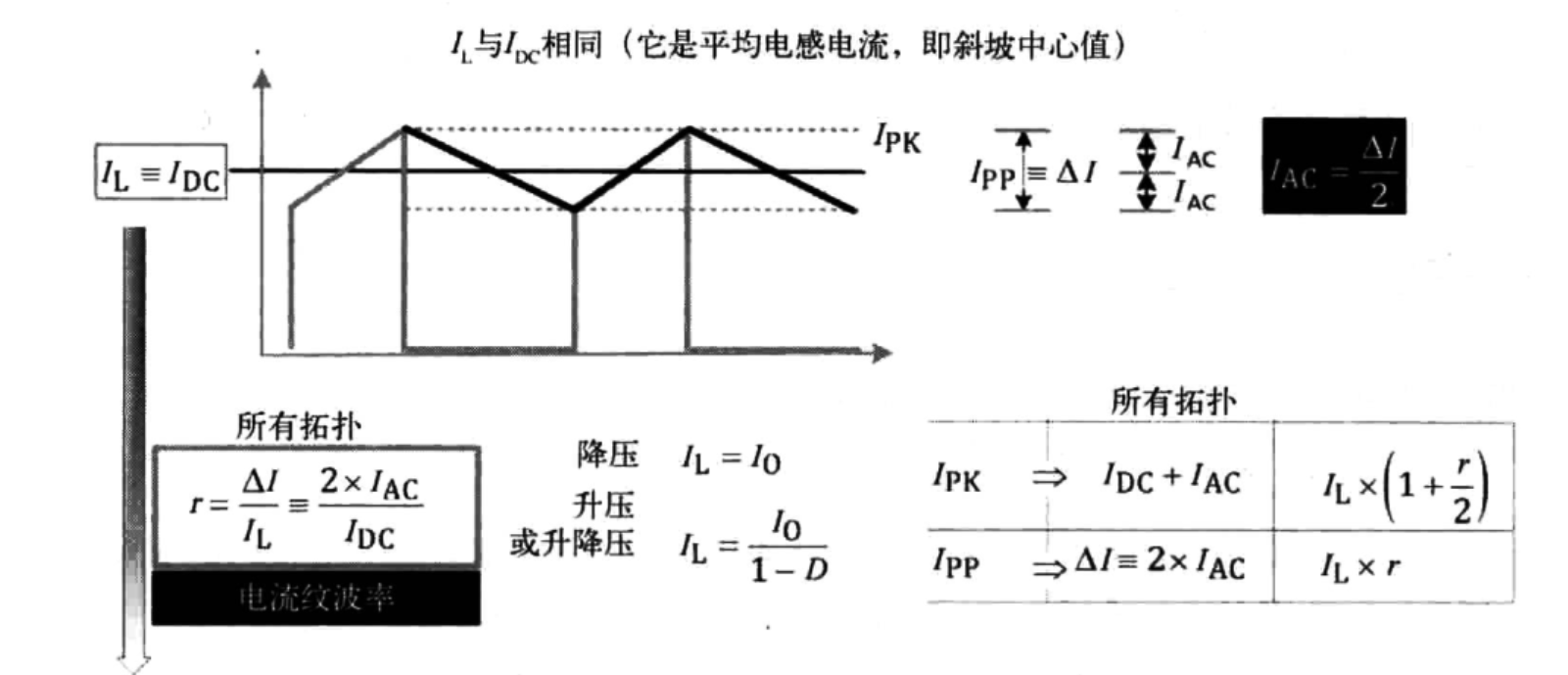
电感电流的交流值定义
$$I_{\mathrm{AC}}=\frac{\Delta I}{2}$$
峰值电流定义
$$I_{\mathrm{PK}}=I_{\mathrm{DC}}+I_{\mathrm{AC}}$$
在所有的电流分量中,峰值电流是最重要的,它不仅是长期热积累和温升的源头,还是开关瞬间损坏的原因:
电流达到峰值时,电感内的磁场强度也会达到峰值,可能会发生磁路饱和,而一旦发生磁芯饱和,就会有几乎不可控的电流流过开关管
2.4 理解交流、直流和峰值电流
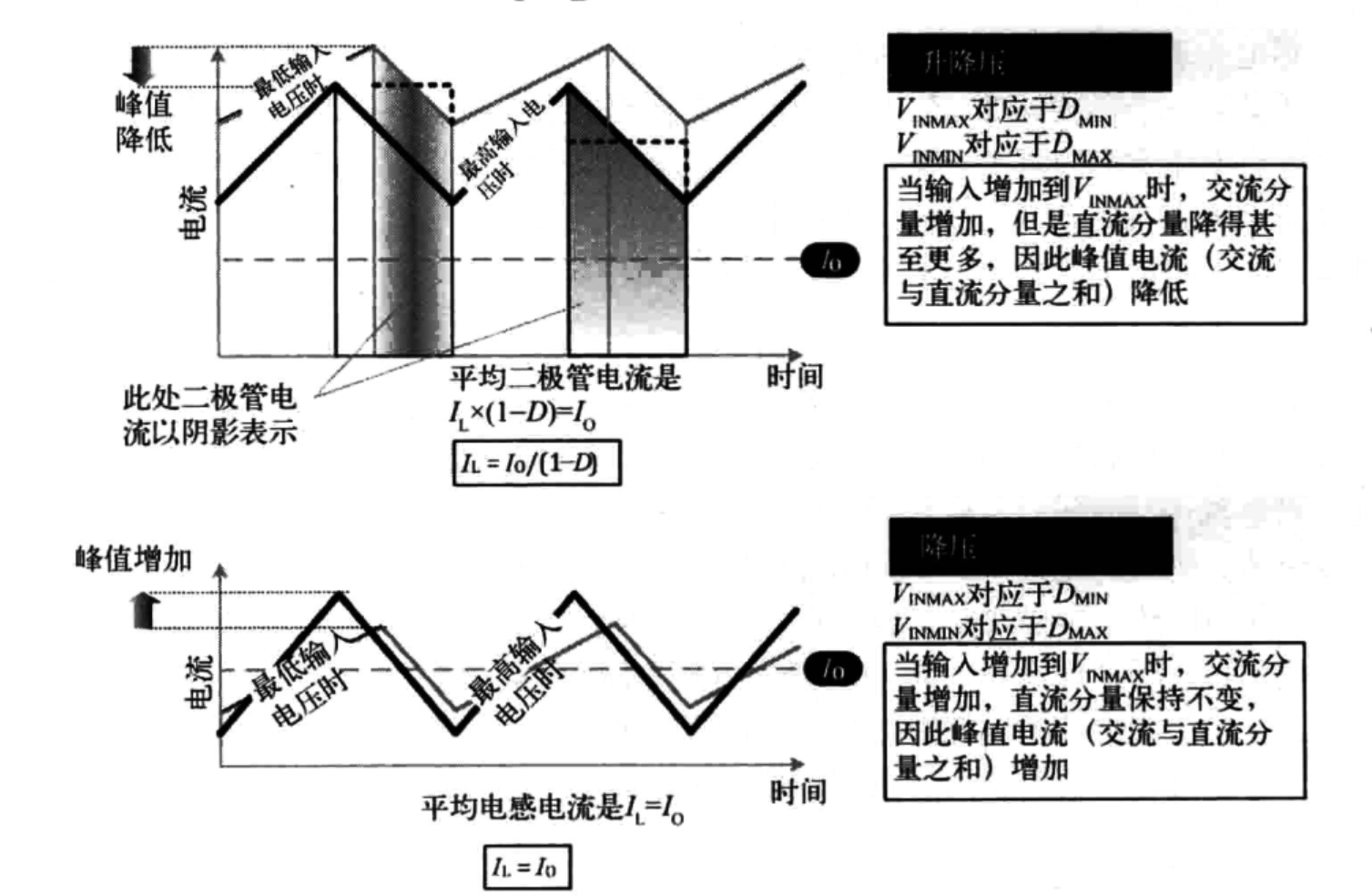
[[第二章 DC-DC变换器及其磁性元件设计#2.2 电感电流波形中的直流分量和交流分量]]
2.5 定义“最恶劣”输入电压
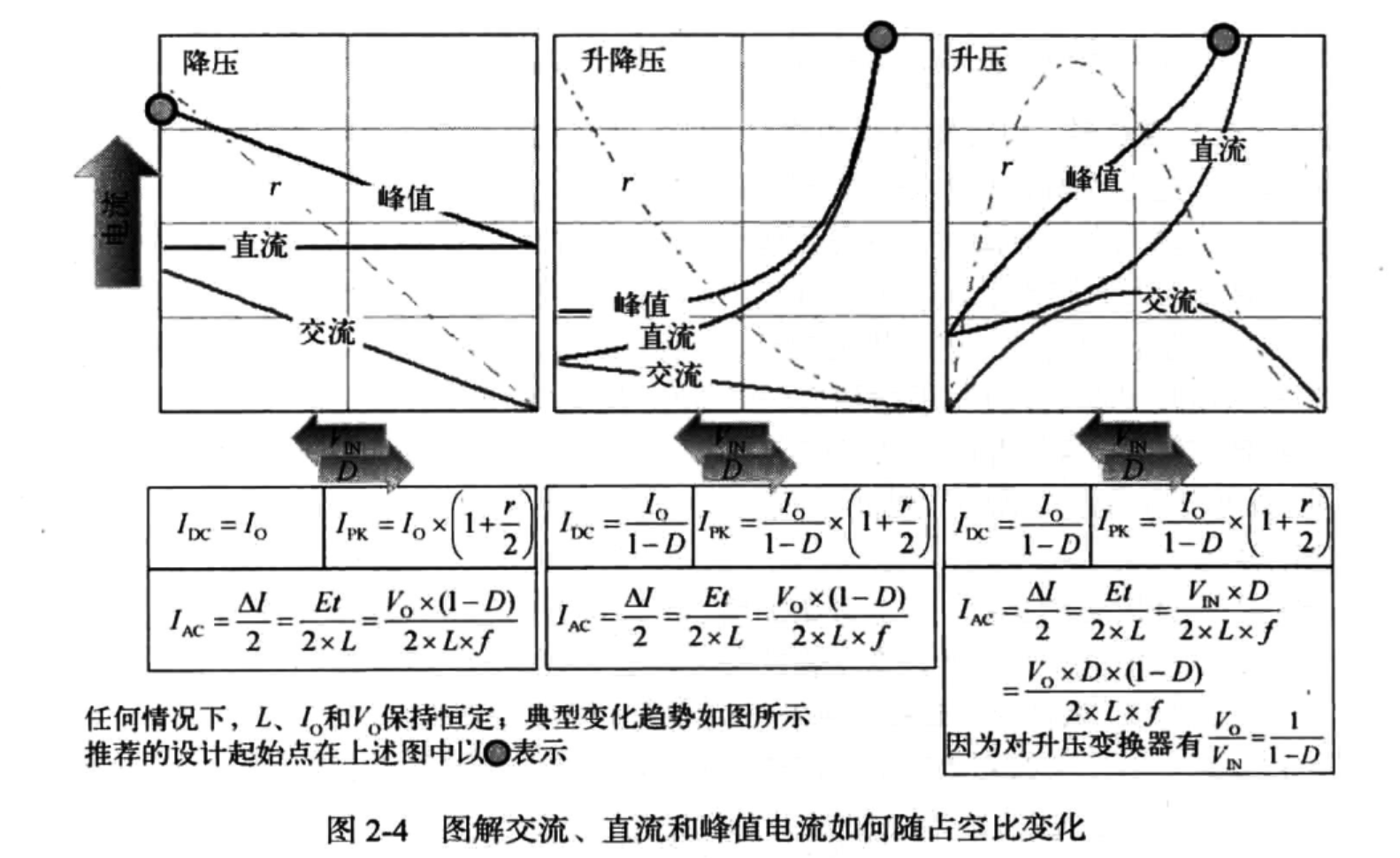
对于降压变压器
总是从$V_{INMAX}(D_{MIN})$开始设计电感
对于升降压变换器
总是从$V_{INMIN}(D_{MAX})$开始设计电感
对于升压变换器
总是从$V_{INMIN}(D_{MAX})$开始设计电感
2.6 电流纹波率r
$$r=\frac{\Delta I}{I_{\mathrm{L}}}\equiv2\times\frac{I_{\mathrm{AC}}}{I_{\mathrm{DC}}}$$
2.7 r与电感值的关系
$$r=\frac{Et}{(L\times I_{\mathrm{L}})}\equiv\frac{V_{\mathrm{ON}}\times D}{(L\times I_{\mathrm{L}})\times f}\equiv\frac{V_{\mathrm{OFF}}\times(1-D)}{(L\times I_{\mathrm{L}})\times f}(\text{所有拓扑})$$
仅限于连续导通模式
简易形式——LI方程
$$L\times I_{\mathrm{L}}=\frac{Et}{r}(\text{所有拓扑 })$$
一般情况下,先设定r再计算L,且r在0.3~0.5,最好取0.4
2.8 r的最优值
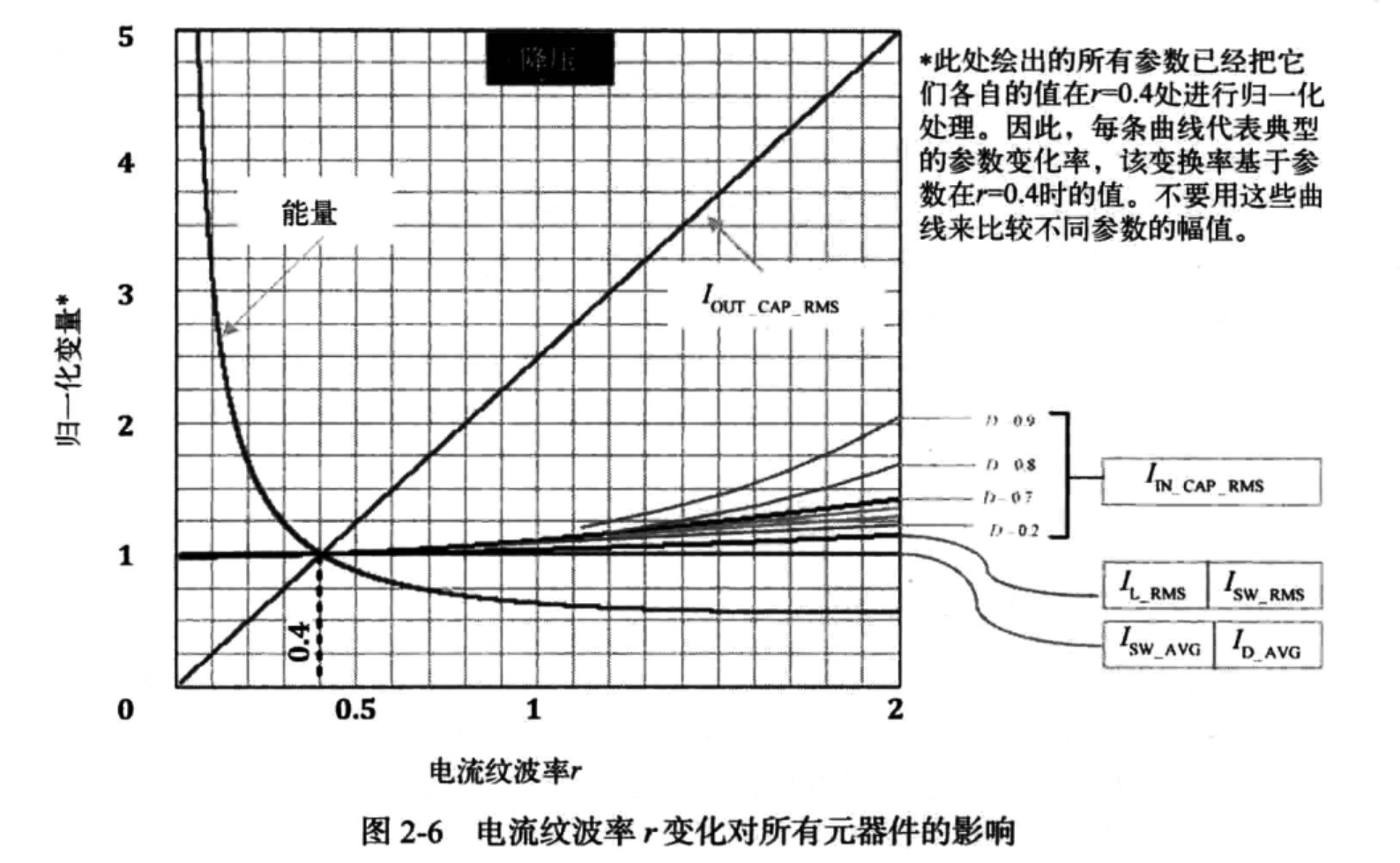
由图可以看出,r在0.4时能够在最小电感值(电感体积)下满足电感处理能量的要求
2.9 是电感尺寸还是电感值
电感尺寸和电感值不一定相关,但一般情况下认为其正相关
2.10 负载电流对电感值和电感尺寸的影响
一般认为电感值和负载电流成反比,电感尺寸和负载电流成正比
因为负载电流影响电感直流量$I_{DC}$大小,从而影响r大小,为了使得r始终存在于最佳大小,需要改变电感值大小,即电感尺寸大小
2.11 供应商如何标定成品电感的额定电流、以及如何选择电感
$I_{DC}$额定值和$I_{RMS}$一般定义为额定温升下(由厂商确定)允许通过的直流电流大小
$I_{SAT}$表示电感在磁芯饱和前允许通过的最大电流,一般认为此时电感储能已接近可用极限
- 一般考虑所有标定电流额定值中最小的
2.12 给定应用中需要考虑的电感电流额定值
在变换器启动或者遭遇电网及负载突变时,电流无法保持正常运行,此时电感可能饱和,但限流电路工作足够快防止开关芯片损坏
此处需要理解足够快到底有多快,响应时间
- 任何限流电路都有一定响应时间,信号的传导延时
- 若MOS不集成,则开关芯片控制信号由于线路物理距离产生寄生电感产生时延
- MOS寄生电容参数在开关改变状态前的充放电影响MOS开关速度,这点在并联MOS通过大电流时尤为明显
- 控制芯片内置的消隐时间导致的开关时延
- 集成高频开关管(MOS或BJT与控制器和驱动器集成在同一封装中)集成电感最小,最可靠,同时消隐时间可以设置更精确更优化
- 在离线运用中,使用足够大磁芯以避免在电流限制处达到饱和
- 低压($V_{IN}<40V$)仅根据最大电流选择电感,虽然很多情况下并未解释原因,但似乎很奏效
2.13 电流限制的范围和容限
- 要保证输出功率,只需考虑电流限制的最小值,即峰值电流小于限制电流最小值
- 由于电感容限一般为+-10%,需要在电感选型时比计算值大10%
- 也要在峰值电流和限制电流最小值之间留出最小20%的额定余量
- 只有在电感饱和被认为是真正值得关注的时候(如高电压应用),电流限制最大值才必须予以考虑
2.14 实例(1)

首先求最劣工况下的占空比
$$D=\frac{V_{\mathbf{O}}-V_{\mathbf{IN}}}{V_{\mathbf{0}}}=\frac{24-12}{24}=0.5$$
再据此计算电感电流和峰值电流
$$I_{\mathrm{L}}=\frac{I_{\mathbf{O}}}{1-D}=\frac{2}{1-0.5}=4\mathrm{A}$$
$$I_{\mathbf{PK}}=I_{\mathrm{L}}\left(1+\frac{r}{2}\right)=4\times\left(1+\frac{0.4}{2}\right)=4.8\dot{\mathbf{A}}$$
并根据前导公式进行电感量的计算[[第二章 DC-DC变换器及其磁性元件设计#2.7 r与电感值的关系|前导公式]]
$$L=\frac{V_{\mathrm{ON}}\times D}{r\times I_{\mathrm{L}}\times f}=\frac{12\times0.5}{0.4\times4\times100\times10^{3}}\Rightarrow37.5\mu\mathrm{H}$$
2.14.1 设置r时对电流限制的考虑
由于选型器件的限制(电流限制最小值),r不可能一直为0.4,且升压、降压芯片由于$I_{O}/=I_{L}$,对$I_L$有更大的芯片电流要求
2.14.2 r固定时,对连续导通模式的考虑
尽量不要使电路再断续导通模式下工作
相同的$\Delta I$下,较小的$I_O$会使电感电流进入断续导通模式
若有最小负载则$I_{AC}<=I_{LMIN}$
让变换器进入断续导通模式的一般方法:
- 减小负载
- 选择小电感
- 增加输入电压
2.14.3 使用地等效串联电阻的电容时,r值应大于0.4
当有MLCC电容时由于出色的小等效串联电阻,能够流过纹波能力加强,从而可以通过增大r减小电感大小减小电感尺寸
2.14.4 设置r值以避免特殊器件带来的问题
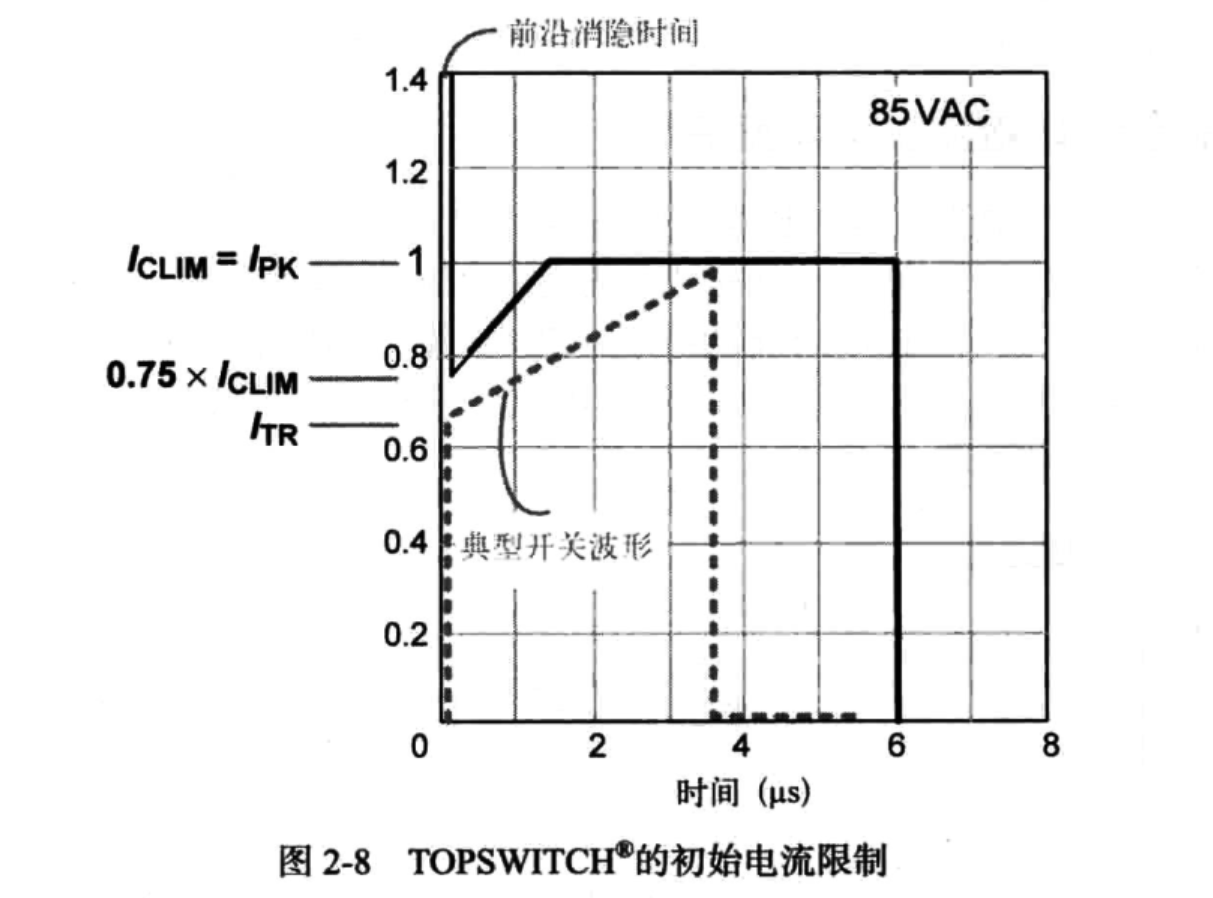
由于部分芯片再导通暂态结束后电流限制会在一段时间内变化,需要电路电流波谷低于这个下降的电流限制,以本图为例
$$I_{\mathrm{TR}}=I_{\mathrm{L}}\times\left(1-\frac{r}{2}\right)$$
$$I_{\mathrm{TR}}=I_{\mathrm{L}}\times\left(1-\frac{r}{2}\right)\leqslant0.75\times I_{\mathrm{CLM}}$$
$$I_{\mathrm{PK}}=I_{\mathrm{L}}\times\left(1-\frac{r}{2}\right)=I_{\mathrm{CLIM}}.$$
$$\left(1-\frac{r}{2}\right)\leqslant0.75\times\left(1+\frac{r}{2}\right)$$$$r\geq0.286$$
一般r设置再0.4所以通常不会特别麻烦
2.14.5 设置r值以避免次谐波震荡
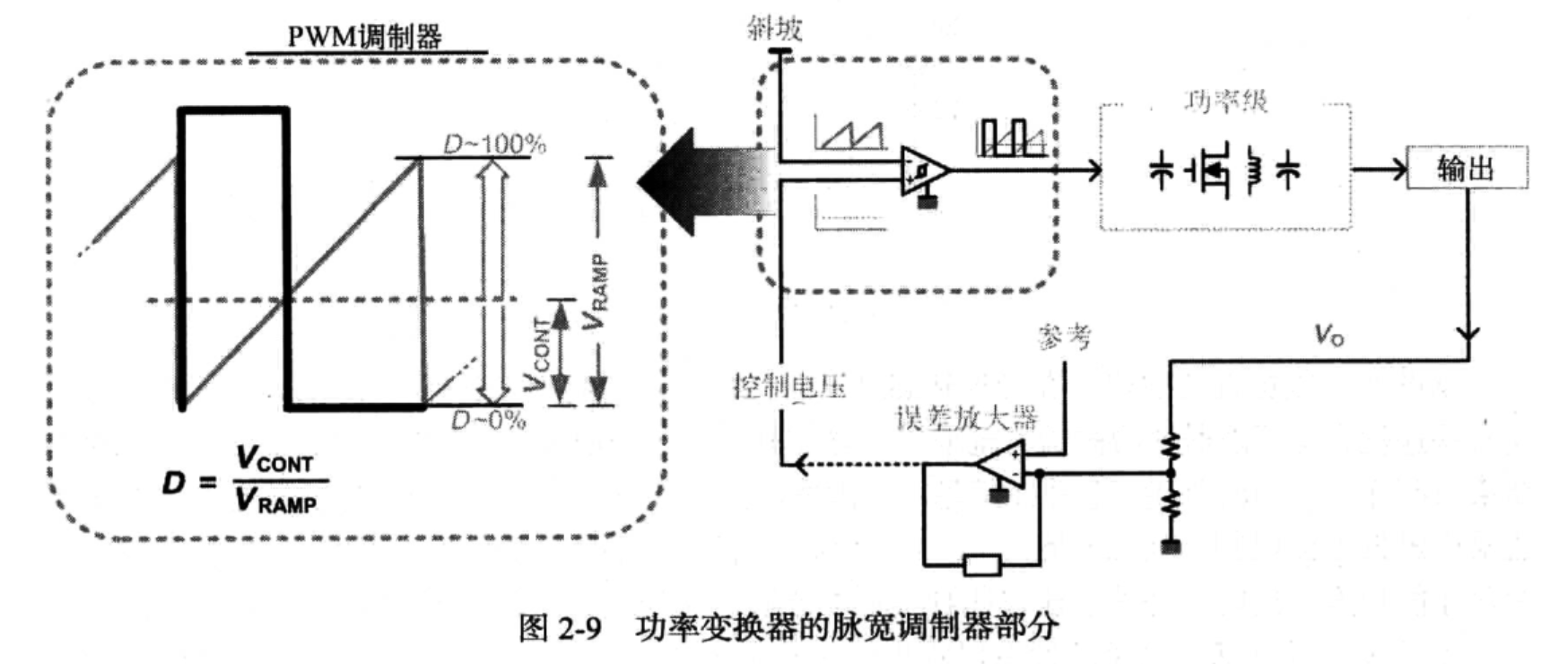

在变换器电压控制时,PWM比较器比较源是比较器内部固定斜坡时钟和输出电压之间的比较
在电流控制室,PWM比较器可能会在电感电流收到轻微扰动之后产生愈来愈大的误差
解决办法:
- 在采样电压斜坡上叠加一个小的固定电压斜坡
- 从控制电压输出中减去同样的电压斜坡
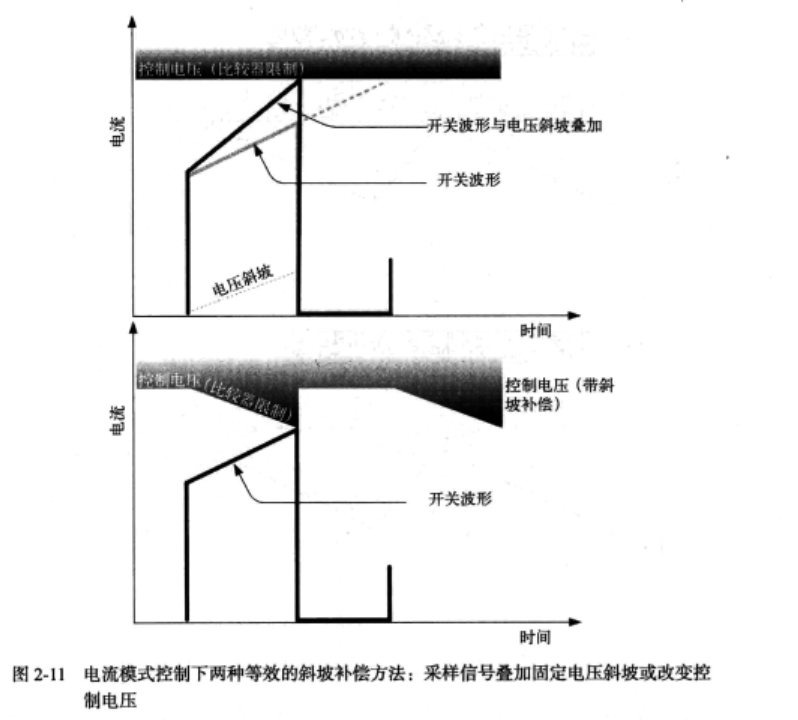
详见19章
2.14.6 使用L * I 和负载所方法快速选择电感
使用[[第二章 DC-DC变换器及其磁性元件设计#2.7 r与电感值的关系|前导公式]]快速推导
$$(L\times I_{\mathrm{L}})=\frac{Et}{r}\left(\text{ 所有拓扑 }\right)$$
2.15 实例(2、3和4)






2.15.1 强迫连续导通模式下的电流纹波率r
详见第9章
同步整流变换器!
2.15.2 基本磁定义(电磁场)
MKS单位制,也称SI国际单位制
基本定义如下
- H: 磁场强度、磁场密度、此话里、外加场等,单位A/m
- B: 也称磁通密度或磁感应强度,单位T或Wb/m2】
- 磁通量: 是B在特定表面面积上的积分,单位是Wb
$$\phi=\int\limits_{S}B\mathrm{d}S_{\mathrm{Wb}}$$ - 任意点上$B=\miu H$,其中u是磁性材料的磁导率,且u表示相对磁导率,即磁性材料磁导率和空气的磁导率之比,通常写作$u_c=uu_0$
- 电感电压和磁通密度关系-法拉第电磁感应定律(楞次定律)
$$V=N\frac{\mathbf{d}\phi}{\mathbf{d}t}=NA\frac{\mathbf{d}B}{\mathbf{d}t}$$ - 电感定义为
$$L=\frac{N\phi}{I}\mathrm{H}$$ - 电感量和线圈匝数成正比
$$L=A_{\mathrm{L}}\times N^{2}\times10^{-9}\mathrm{H}$$ - 当H沿闭合回路积分时,可用得到回路包围的电流
$$\oint H\mathrm{d}l=I\mathrm{A}$$ - 结合楞次定律
$$V=N\frac{\mathbf{d}\phi}{\mathbf{d}t}=NA\frac{\mathbf{d}B}{\mathbf{d}t}=L\frac{\mathbf{d}I}{\mathbf{d}t}$$ - 得出功率变换中两个重要方程
$$\begin{aligned}\Delta B&=\frac{L\Delta I}{NA}\text{ ( 电流型方程 )}\\\Delta B&=\frac{V\Delta t}{NA}\text{ ( 电压型方程 )}\end{aligned}$$ - 经过变换可得
$$B=\frac{LI}{NA}\text{(电流型方程 )}$$
$$B_{\mathrm{AC}}=\frac{V_{\mathrm{ON}}D}{2\times NAf}\text{(电压型方程 })$$
![[Pasted image 20240323223446.png]]
2.16 实例(5)不增加匝数
在给定应用中,电感值越大,电感尺寸越大,只增加匝数不增加尺寸,会导致电感内磁场强度增加,电感饱和,造成灾难性后果
2.16.1 磁场纹波系数
2.16.2 用伏秒积分析电压型方程
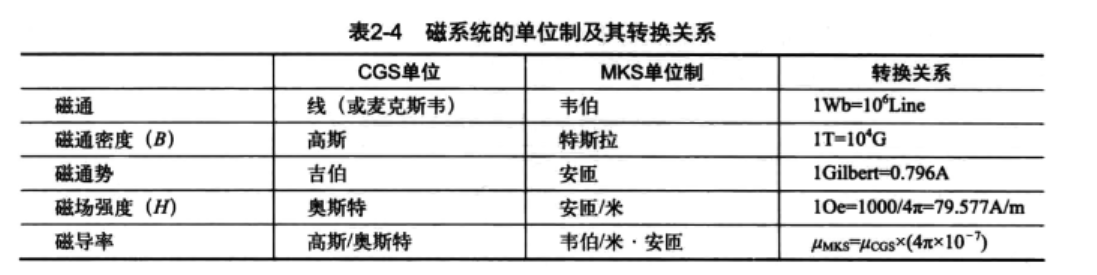
2.16.3 CGS单位制