学习《精通开关电源设计》
目前未能完成hexo对latex的支持,博客公式部分会出现乱码
1.1 引言
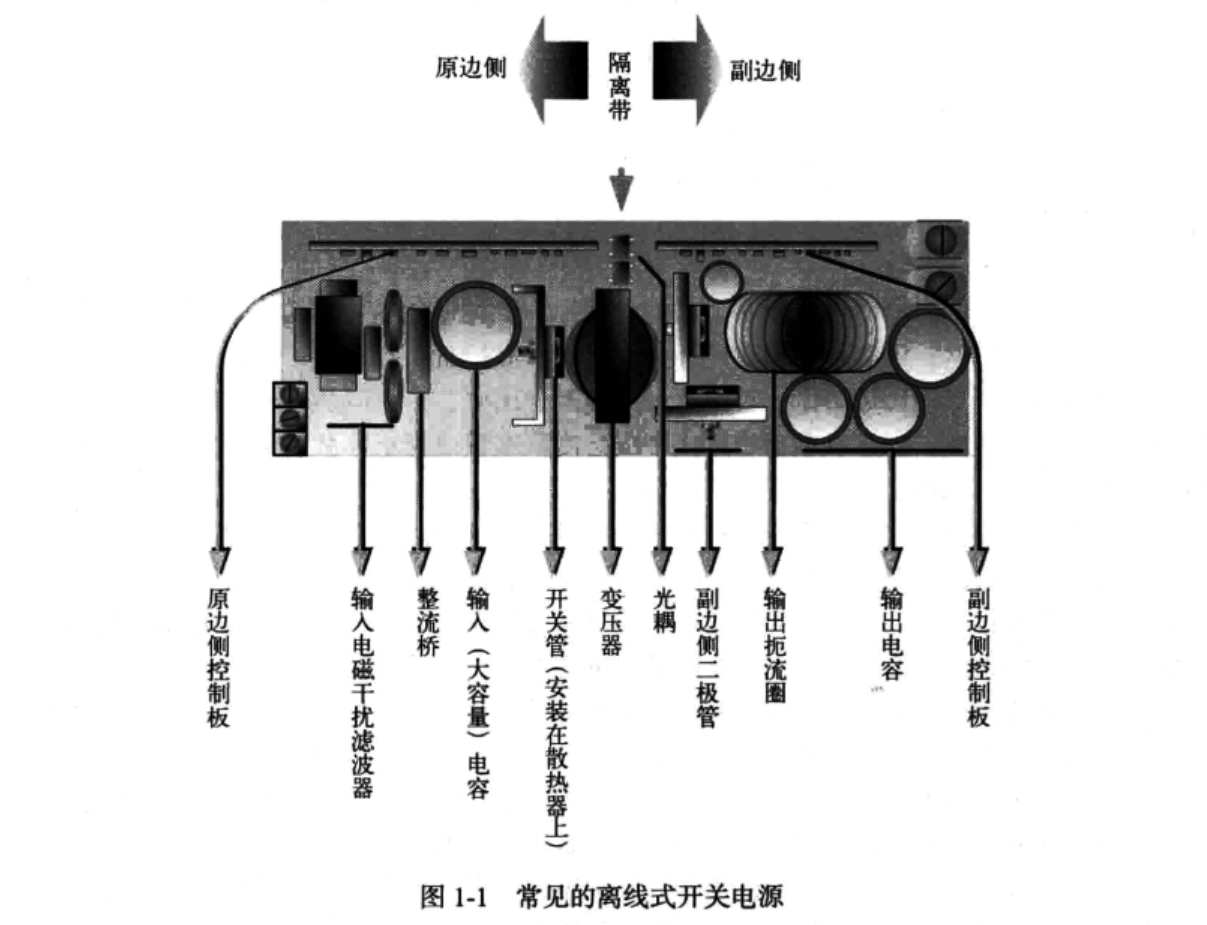
1.2 概述和基本术语
1.2.1 #效率
效率的定义式:
$$\eta=\frac{P_{0}}{P_{\mathrm{IN}}}$$
其中$P_O$是输出功率:$P_{0}=V_{0}\times I_{0}$
其中$P_I$是输出功率:$P_{IN}=V_{IN}\times I_{IN}$
理想状态下开关电源的转换效率为100%,但是实际上不可能达到这么高,现代开关电源的效率一般是65%~95%
1.2.2 线性调整器
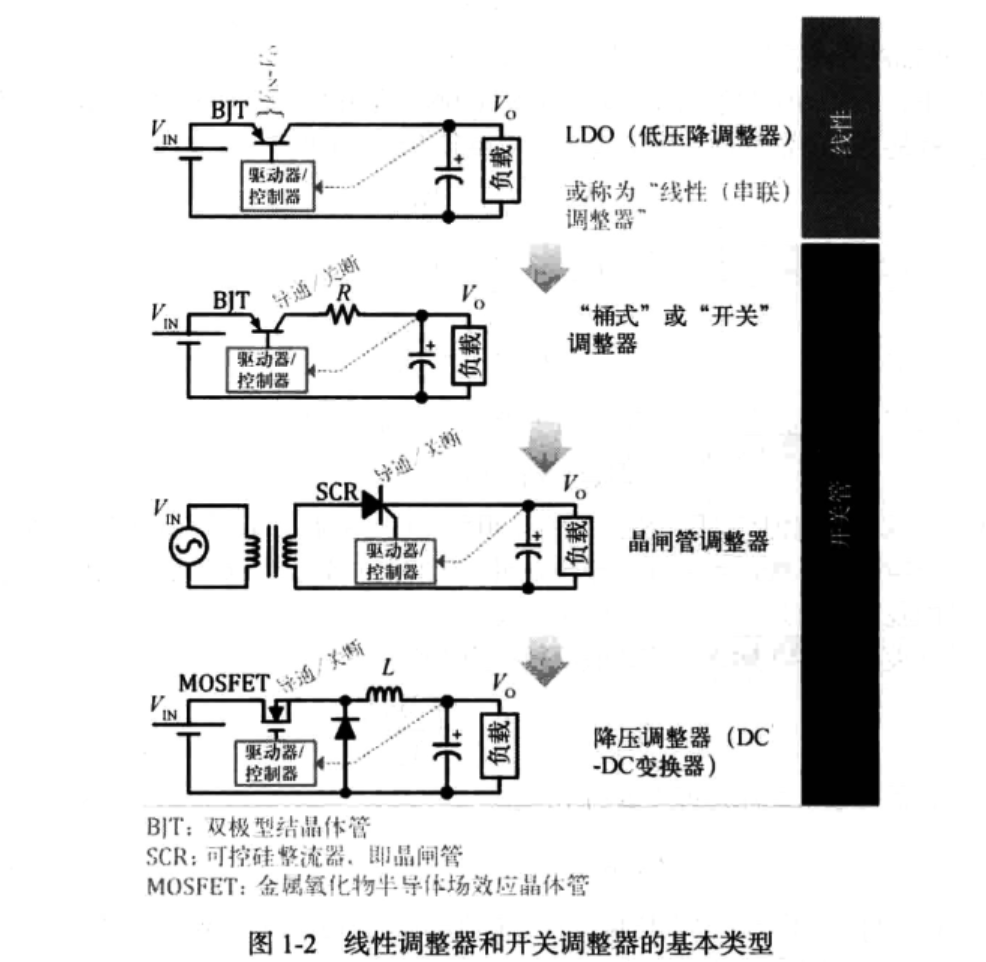
线性调整器也称为串联型调整器,通过使串联的晶体管工作在U-I特性的线性区(可变电阻)完成降压,实际上是将降压部分的功耗消耗在了串联晶体管上。
其缺点是效率低,优点是无噪声问题和EMI问题
1.2.3 利用开关器件提高效率
开关器件工作在开关模式而非放大模式,理想状态下无开关损耗
1.2.4 半导体开关器件的基本类型
BJT(双极性晶体管)
速度慢但价格低廉,其中NPN价格更低更广泛应用
MOSFET(金属氧化物半导体场效应晶体管)
其中NMOS和PMOS最常用,而且NMOS高性价比和高性能,而PMOS驱动电路简单
BJT和MOSFET的争论
- MOSFET压控BJT流控(实际上MOS驱动也会有栅极电流,有时为了加速开关会栅极流过更大电流)
- 实际上NPN型BJT导通条件比NMOS更易满足,前者只需要基极电压比发射极电压高0.8V甚至更小,而NMOS需要栅极比漏极高几V才行,于是NMOS驱动会需要自举电路
- BJT开关慢噪声小
- BJT重载下导通压降不变,导通损耗不会随着负载变大
IGBT(绝缘栅型双极晶体管)
主要适合低频大电流
1.2.5 半导体开关器件非理想器件
电子开关损耗:
- 泄露损耗: 关断时漏电流产生的损耗
- 导通损耗: 导通时产生正向压降产生的损耗
- 开关损耗/交叉损耗: 开关转换时电压电流交叉产生的损耗
1.2.6 利用电抗元件提高效率
现代开关电源效率高的另一原因时电容和电感的有效使用
开关电源的+工作逻辑
- 使用开关管来简历输出电压控制
- 每次开关动作都能有效断开输入和输出
- 一旦引入电容,就需要限制其过大的浪涌电流(直流电输入电容的UI特性)–会增大噪声电磁干扰和降低效率
- 为提高效率使用电感元件进行限流并进行能量储存释放
1.2.7 早期RC型开关调整器

1.2.8 LC型开关调整器
其他开关调整器
- 电荷泵: 仅限于小功率使用
- 谐振型: 工频变化大不可控噪声问题
1.2.9 寄生参数影响
电抗元件的温升总源自元件自身与生俱来的小阻值寄生电阻的损耗
EG:
- 电感寄生的直流电阻DCR
- 电容寄生的等效串联电阻ESR
而其他元器件也具有各种不同的寄生电抗参数
寄生参数不是完全有害的,他们对电路稳定性又是十分有益
EG:
- 短路故障下寄生参数遏制短路电流的过大
- 输出电容等效串联电阻减小调整输出时的过度震荡和振铃
- 寄生电感在开关导通时限制剑锋电流,但在关断时会产生尖峰电压
- 寄生电容在关断时有益,导通时有害
1.2.10 高频开关时的问题
1.2.11 可靠性、使用寿命和热管理
延长寿命并提高可靠性的方法是降低开关电源中元器件的温度和电源壳体内的环境温度
1.2.12 应力降频
热应力70%
电气应力70%~80%
一些损耗会随着温度的升高而降低,但温度升高会对系统稳定性产生影响,所以通过提高工作温度来提高效率或者改善性能不可取
1.2.13 技术发展
元器件技术有很大发展,功率变换的基本电路拓扑仍然十分重要
1.3 电感
1.3.1 电容电感和电压电流
要正确认识电感,更多从电流角度出发去认识电路
1.3.2 电感电容的充放电电路
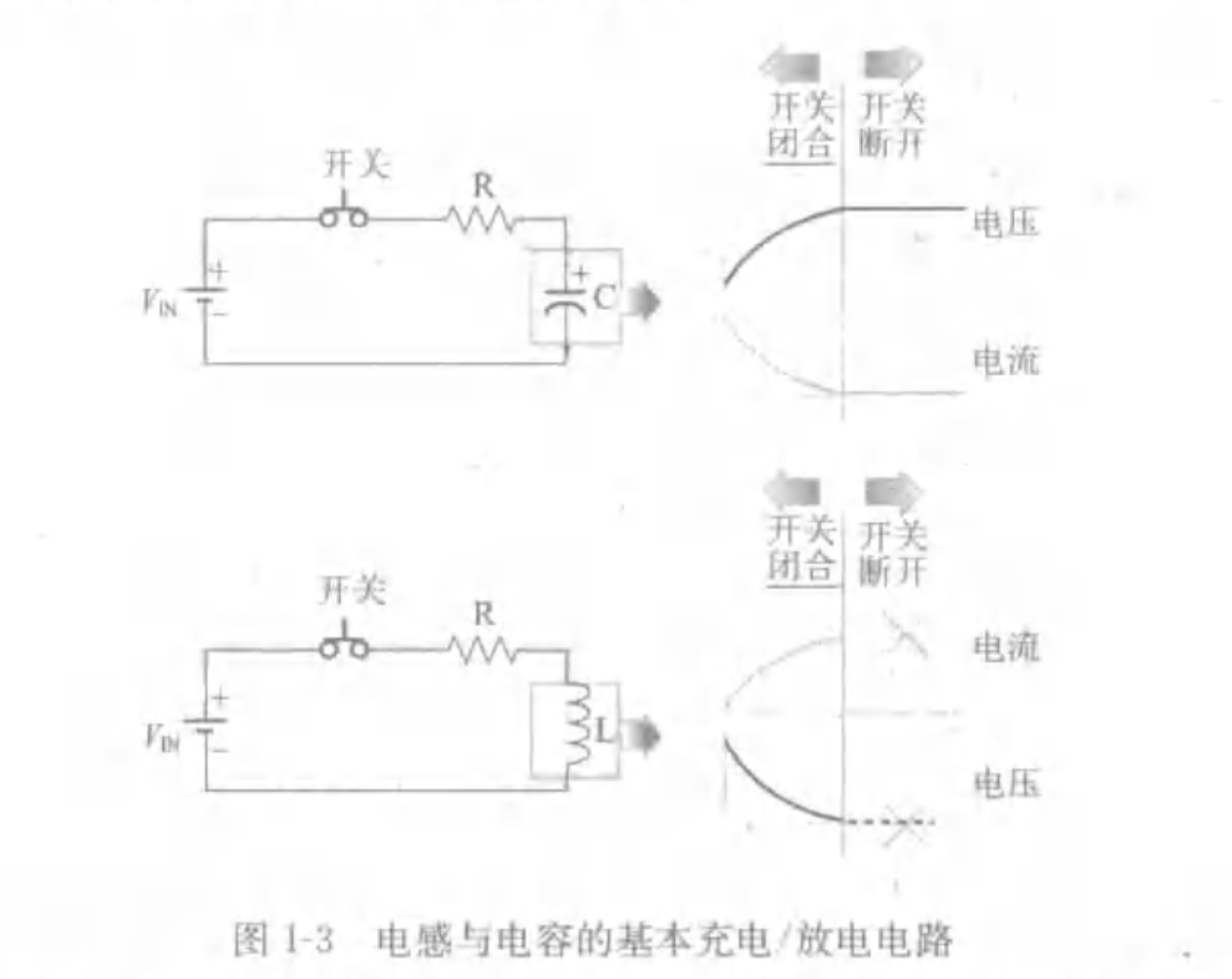
由于电感和电容的对偶特性,很多时候我们可以通过对偶原则来对电感进行定性分析,但图示电感电路和电容电路并不是完全对称的
[[第一章 开关功率变换原理#1.3.7 对偶原理]]
1.3.3 能量守恒定律
1.3.4 充电阶段和感应电压概念
楞次定律和法拉第定律
1.3.5 串联电阻对时间常数的影响
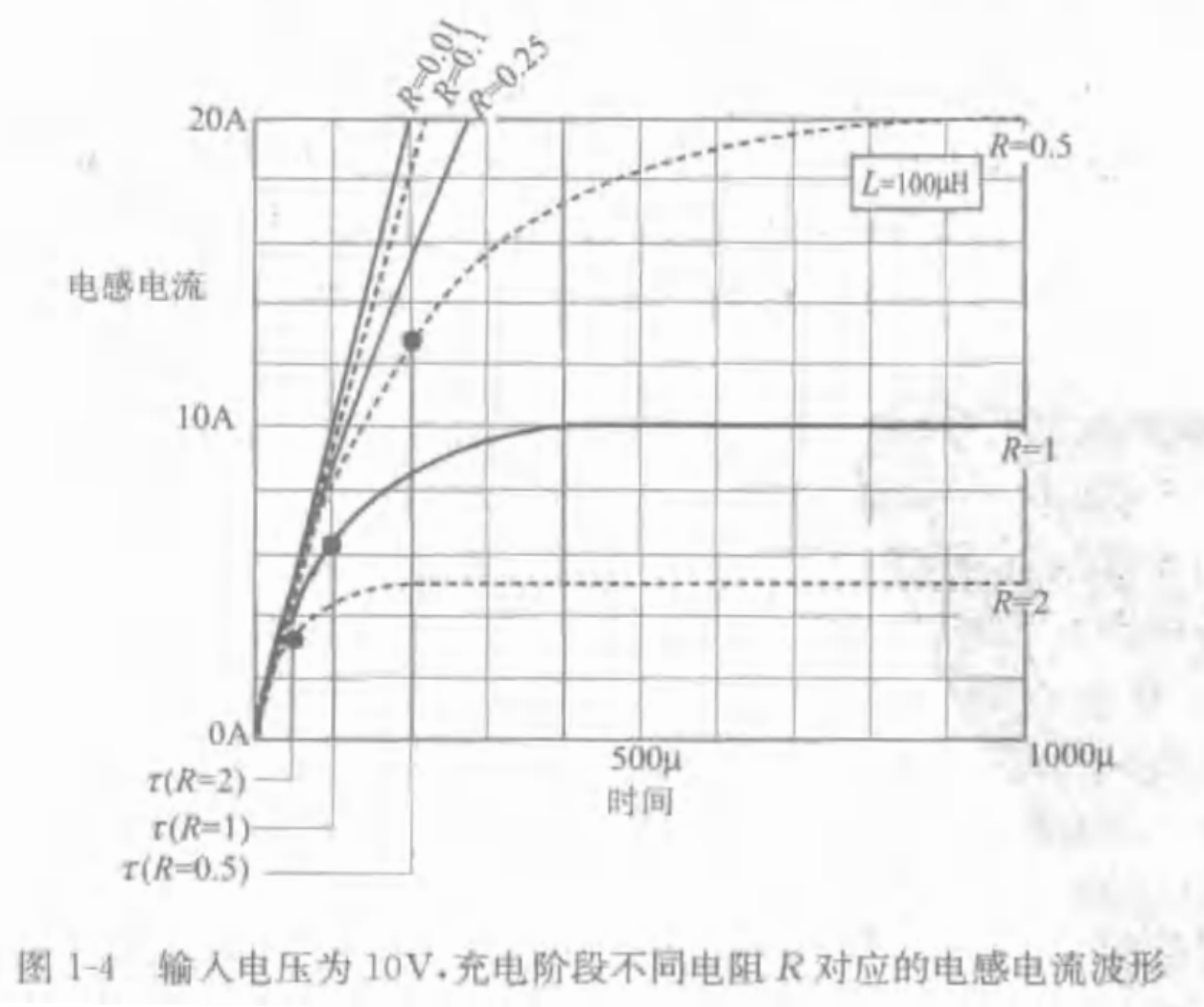
$\tau=L/RL/R$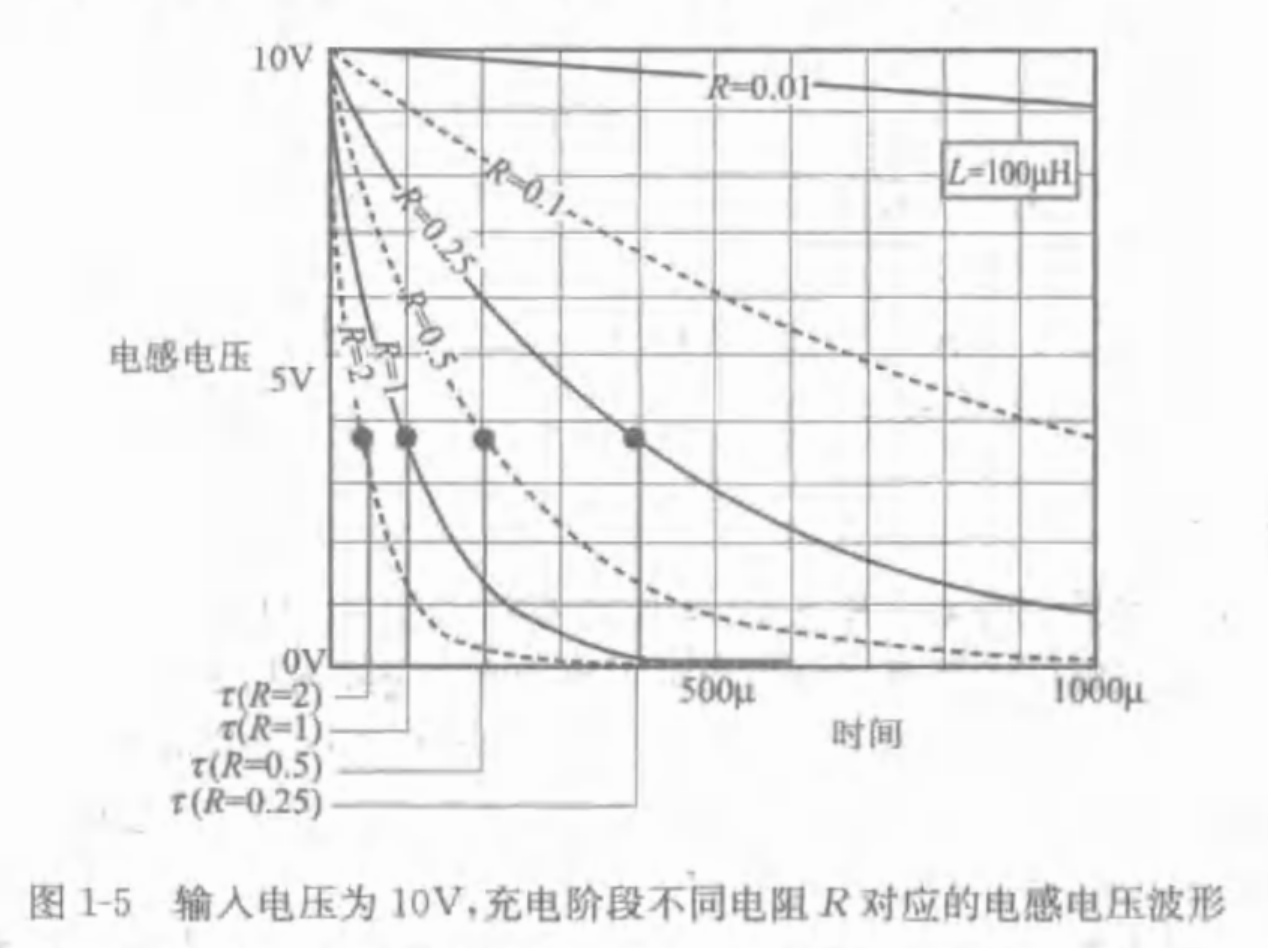
在电感分析中,应该始终注意电感电流变化,电感电压之跟随电流变化
1.3.6 R=0时的电感充电电路和电感方程
$$\frac{\mathrm{d}I}{\mathrm{d}t}=\frac{V}{L}\quad(\text{电感方程})$$
其中电感两侧电压为 V 电流为 I ^1f9f7c
1.3.7 对偶原理
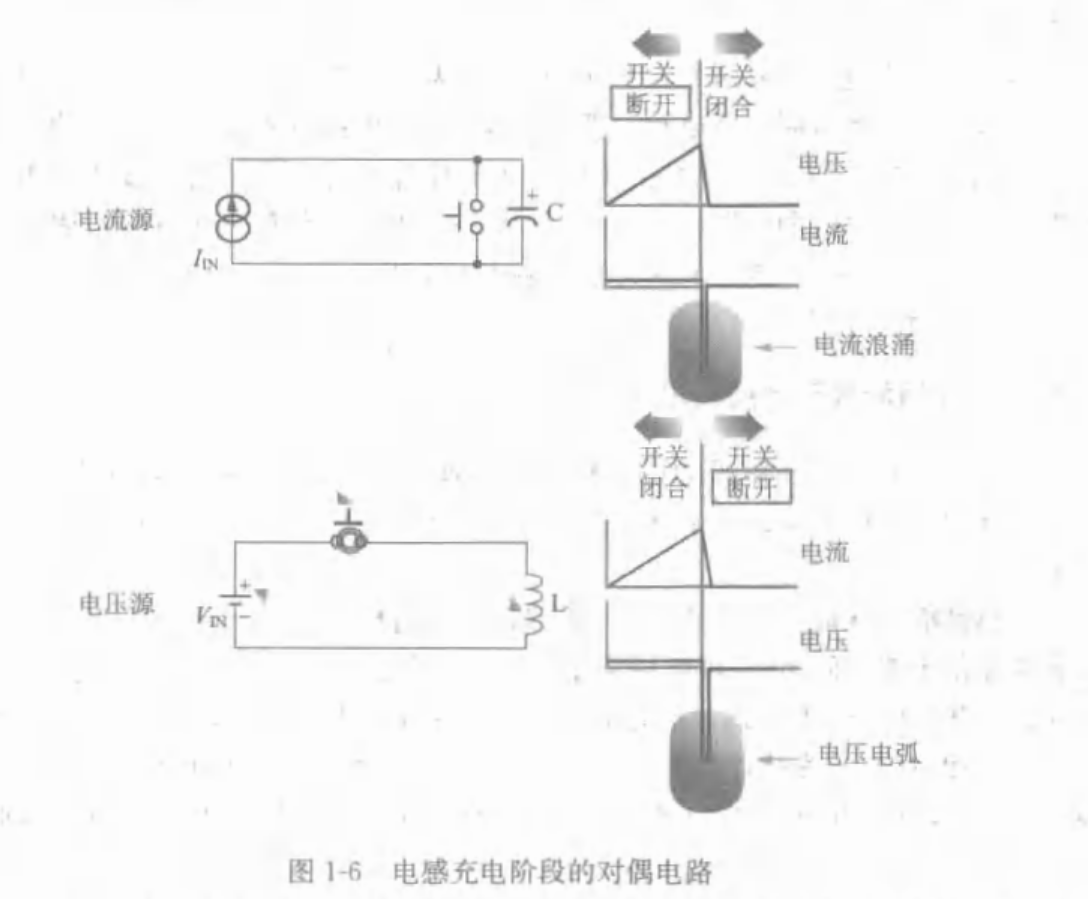
1.3.8 电容方程
$$I=C\frac{\mathrm{d}V}{\mathrm{d}t}(\text{电容方程})$$
1.3.9 电感放电阶段
1.3.10 反击能量和续流电流
1.3.11 电流必须连续,但其变化率未必
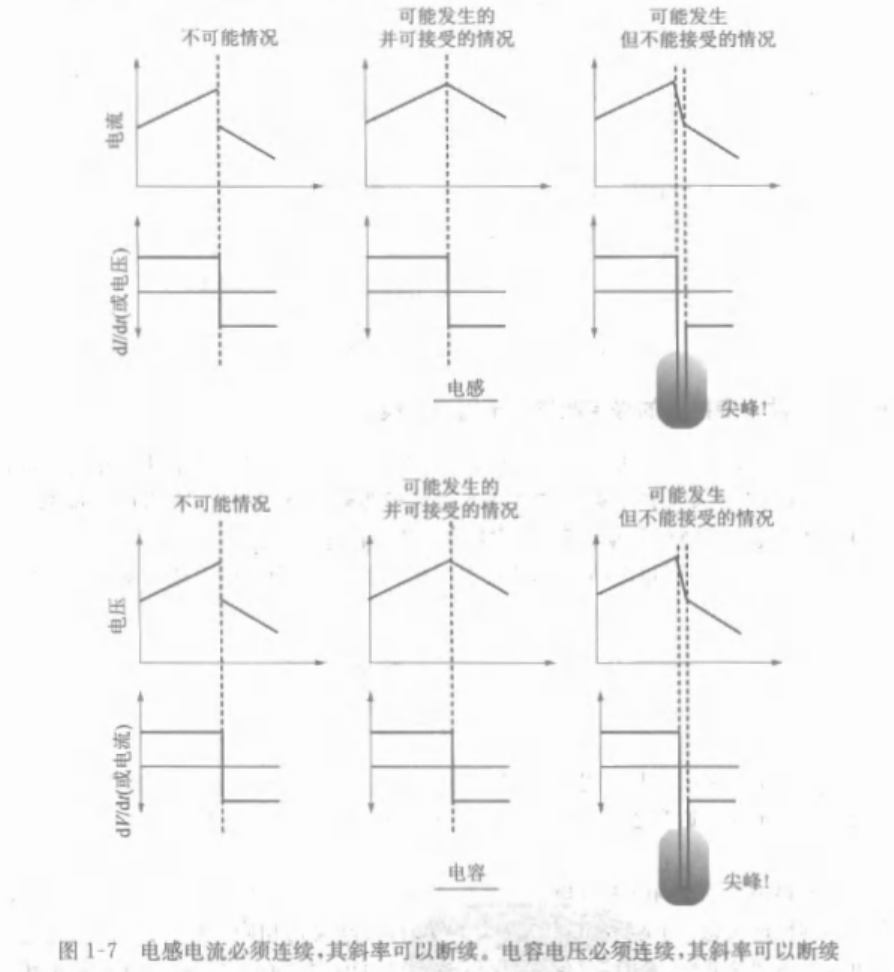
1.3.12 电压反向现象
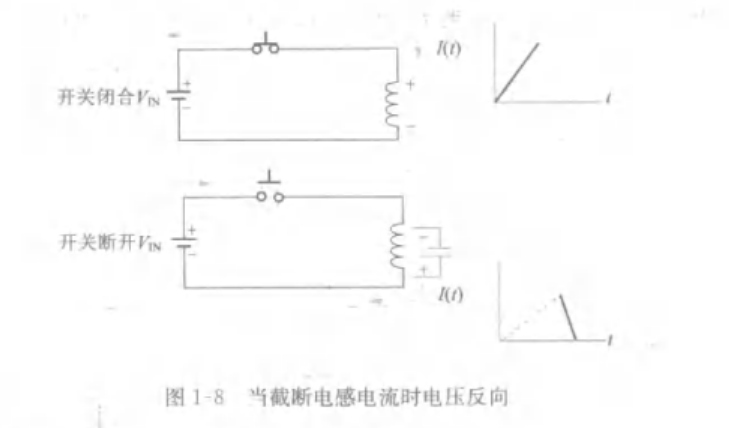
1.3.13 功率变换过程中的稳态及其不同工作模式
![[第一章 开关功率变换原理#^1f9f7c]]
电流在正向电压下上升,在反向电压下下降
在稳态工作状态下,每个周期结束后电流回到开始时的初值
而根据初值的不同,可以将工作模式分为以下几种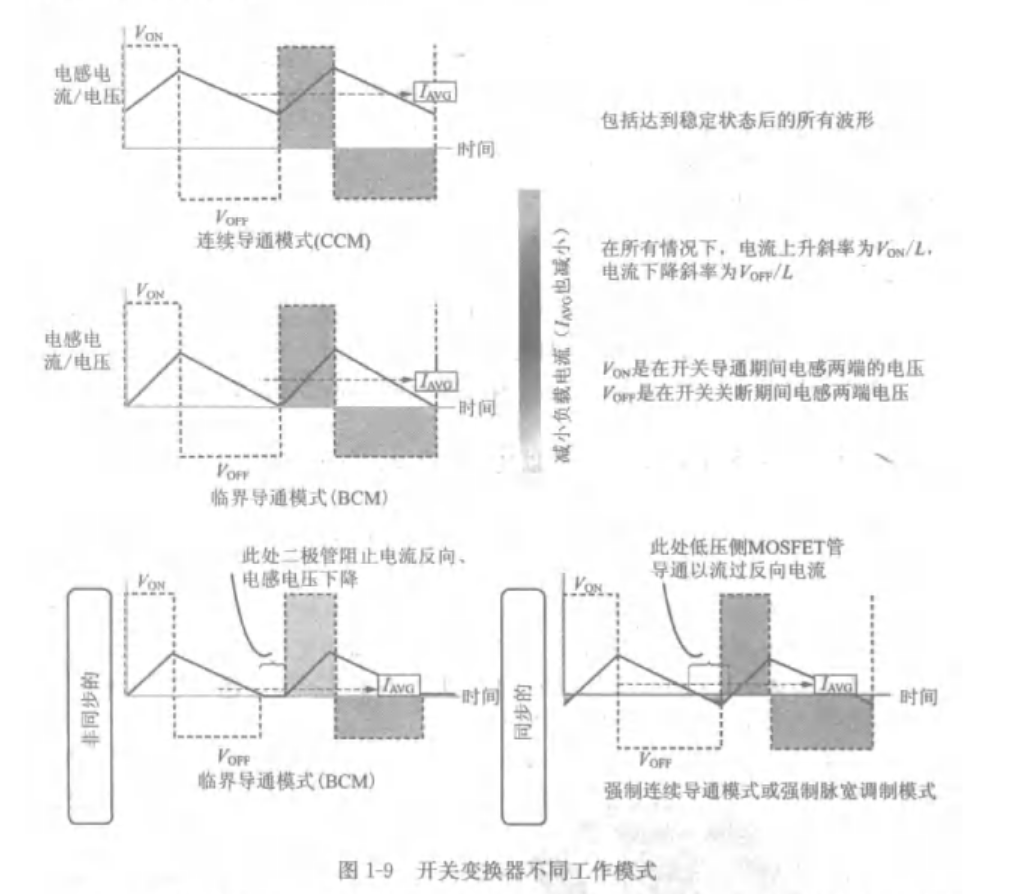
1.3.14 伏秒平衡、电感复位和变换器的占空比
![[第一章 开关功率变换原理#^1f9f7c]]
在一个开关周期内,若电感初值等于末值,有电感电压随时间变化的曲线净面积为0
$$\Delta I_{\mathrm{ON}}=\frac{V_{\mathrm{ON}}\times t_{\mathrm{0N}}}{L}=\frac{V_{\mathrm{ON}}\times t_{\mathrm{ON-uH}}}{L_{\mathrm{uH}}}=\frac{Et}{L_{\mathrm{~\mu H}}}$$
推论: 在稳态工作状态下,每个周期内电感必须复位
$$D=\frac{t_{\mathrm{ON}}}{t_{\mathrm{ON}}+(T-t_{\mathrm{ON}})}=\frac{t_{\mathrm{ON}}}{T}\quad(\text{占空比定义)}$$
需要明确toff指的是感应电压VOFF持续时间而不一定等于开关的管段时间,仅限于连续导通模式下会有:
$$D=\frac{t_{\mathrm{ON}}}{t_{\mathrm{ON}}+t_{\mathrm{OFF}}}\quad\text{(CCM时占空比)}$$
1.3.15 半导体开关器件的使用和保护
- 半导体器件任何工作瞬间哦都不能超过其绝对最大额定电压,否则器件会瞬间损坏
- 不能让期间始终工作在过流状态下
- 需要在设计电路板时设计钳位电路保护
- 需要设置限流保护(下一周期不要记住上一周期发生的事)
1.4 开关拓扑的演变
1.4.1 通过二极管续流控制感应电压尖峰
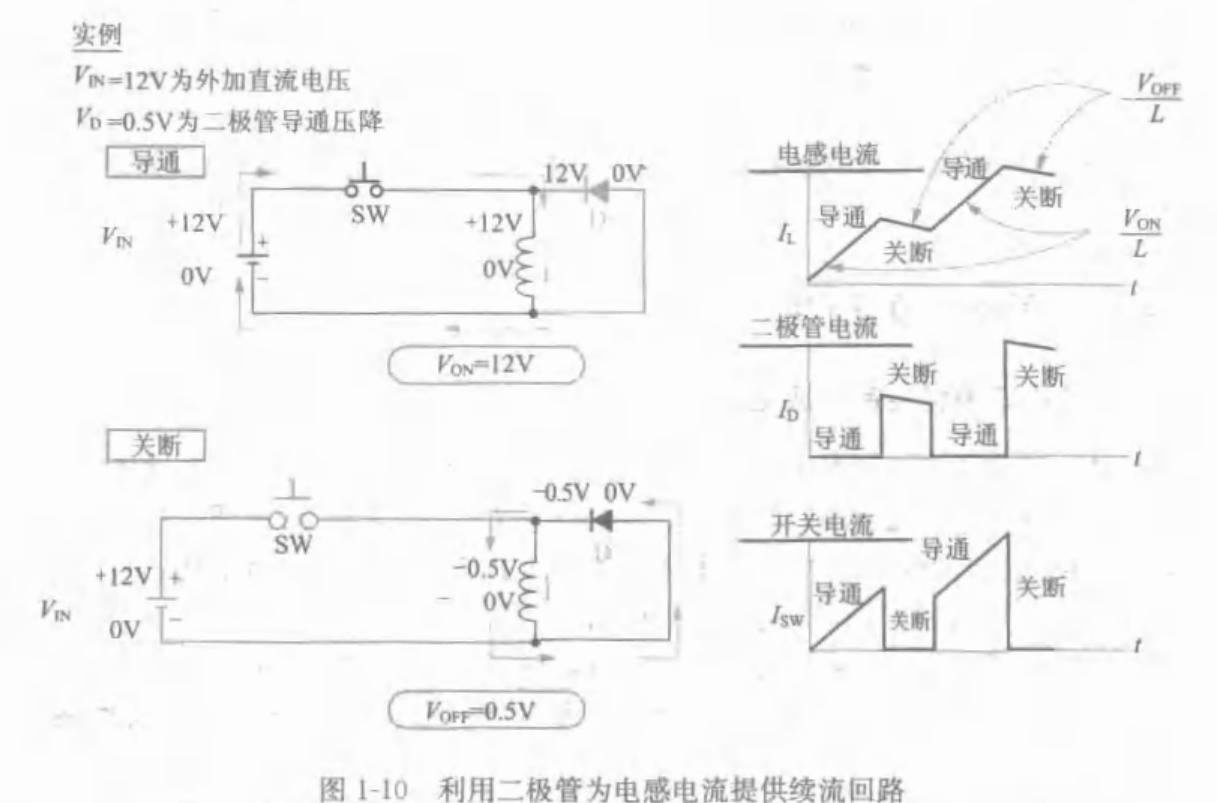
1.4.2 达到稳态并获得有用能量
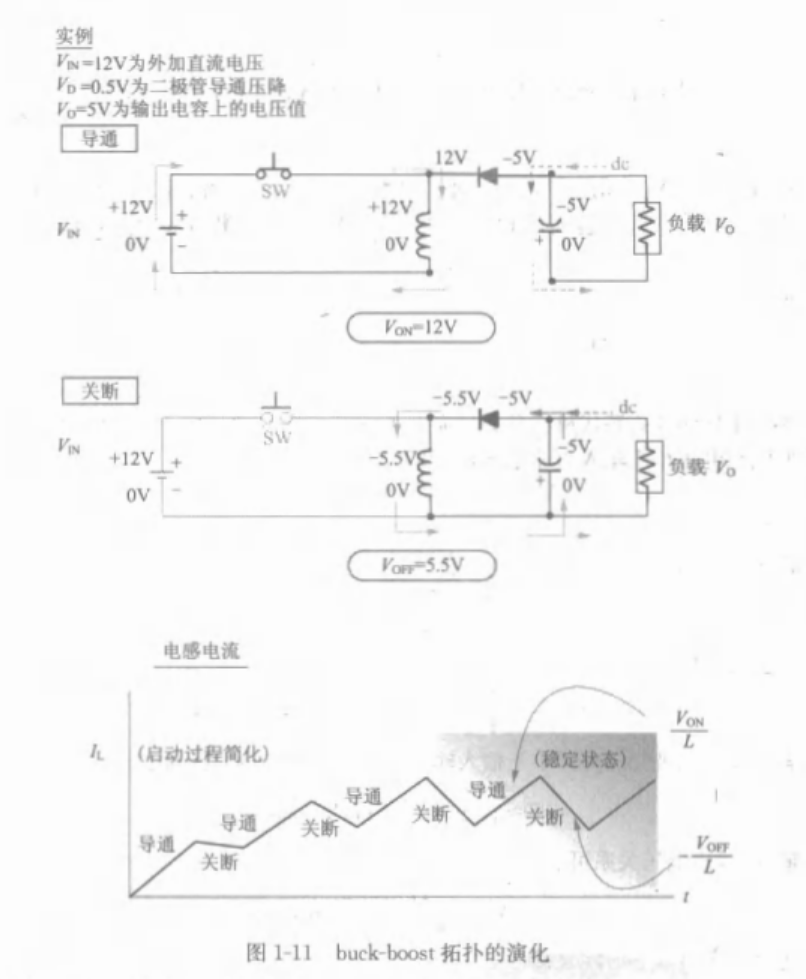
1.4.3 升降压拓扑
半导体开关取代机械开关后,其非零正向压降记为$V_{SW}$,有
$$V_{\mathrm{ON}}=V_{\mathrm{IN}}{-}V_{\mathrm{SW}}\text{(升降压 })$$或$$V_{\mathrm{OFF}}=V_{\mathbf{O}}+V_{\mathbf{D}}\text{(升降压)}$$由伏秒定理可得$$\frac{t_{\mathrm{OFF}}}{t_{\mathrm{ON}}}=\frac{V_{\mathrm{IN}}-V_{\mathrm{Sw}}}{V_{\mathrm{O}}+V_{\mathrm{D}}}\text{(升降压)}$$即$$D=\frac{V_{\mathrm{O}}+V_{\mathrm{D}}}{V_{\mathrm{IN}}-V_{\mathrm{SW}}+V_{\mathrm{O}}+V_{\mathrm{D}}}\text{(升降压 })$$
可以近似于$$V_{\mathbf{0}}=V_{\mathbf{lN}}\times\frac{D}{1-D}\text{(升降压})$$
1.4.4 电路的地参考点
- 在DCDC中输出输入公共导线习惯被称作系统的地
- 另一种惯用表示方法即0V
1.4.5 升降压变换器结构
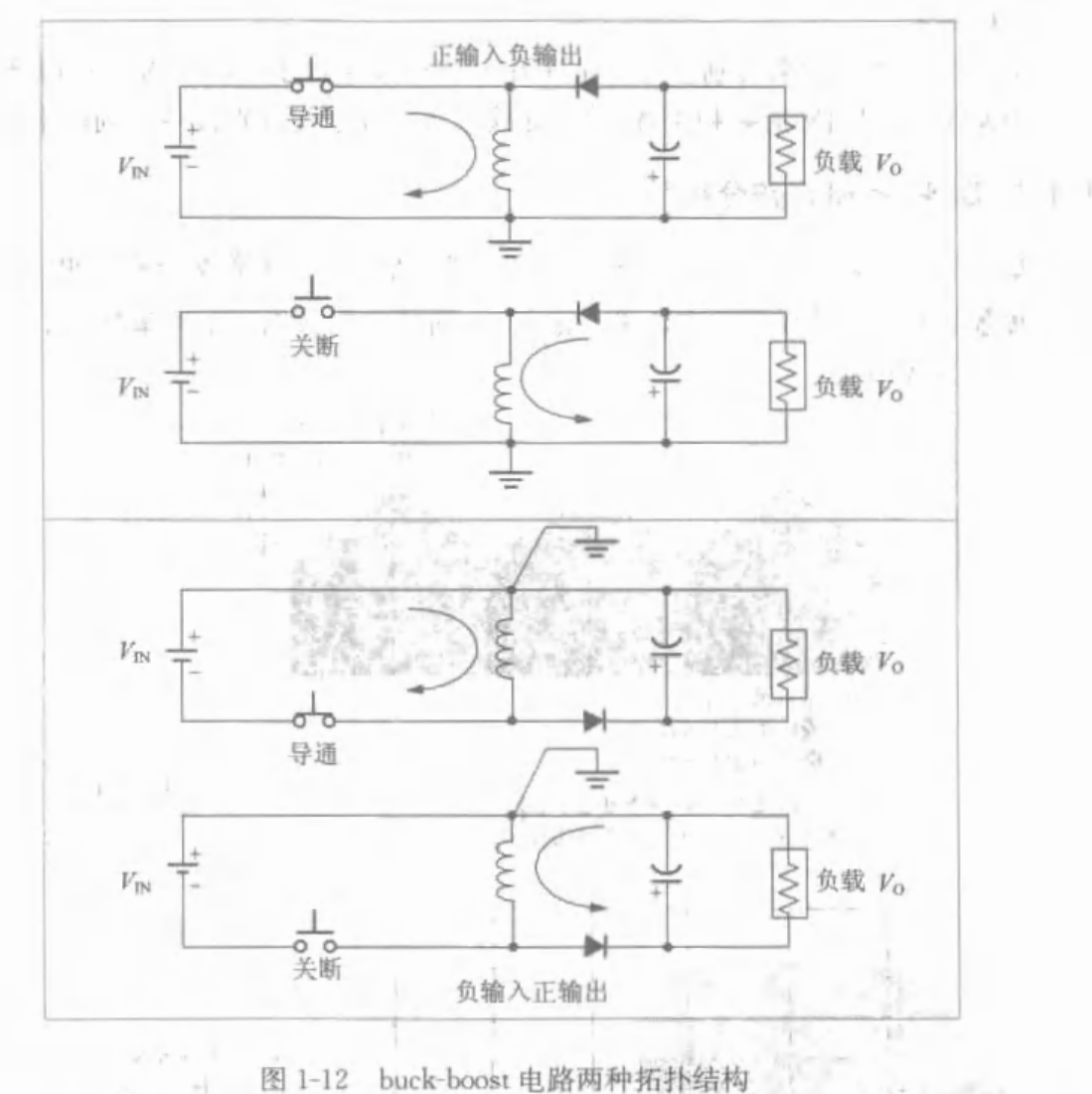
可以看出升降压输出输入的电压极性是相反的,也被称为反极性拓扑
1.4.6 交换结点
电感电流绕行之处,即开关和二极管之间的结点,称为交换结点
SW
设计印制电路板PCB时需要注意,SW引脚()不需要敷太多铜,否则会产生有效的电厂天线,产生射频干扰
1.4.7 升降压变换器分析
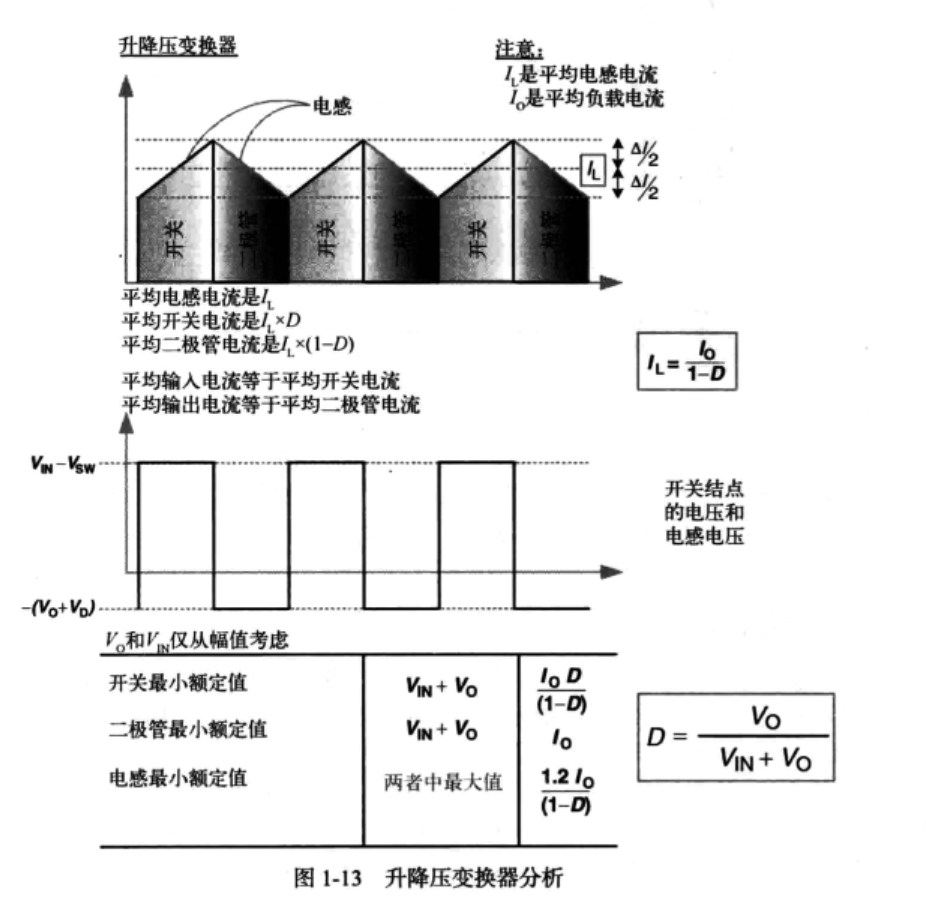
主要关注开关电流、二极管电流和电感电流之间的关系,即
$$\begin{aligned}I_{\mathrm{SW_AVG}}&=I_{\mathrm{L}}\times\frac{t_{\mathrm{ON}}}{T}=I_{\mathrm{L}}\times D&\text{(升降压)}\\I_{\mathrm{D_AVG}}&=I_{\mathrm{L}}\times\frac{t_{\mathrm{OFF}}}{T}=I_{\mathrm{L}}\times D^{\prime}=I_{\mathrm{L}}\times(1-D)&\text{(升降压)}\end{aligned}$$
1.4.8 升降压变换器特性
- 输出输入电压极性相反,可以升降压变换
- 开关导通时,能量流入电感
- 开关断开时,能量通过二极管输出给负载
- 升降压时唯一纯反激拓扑,没有能量直接从电源输出给负载
- 升降压变换器的效率不是很高,噪声纹波也比较大,可能需要在变换器输入端外加滤波器
1.4.9 为什么仅有三种基本拓扑
分类方式:电感的接入方式: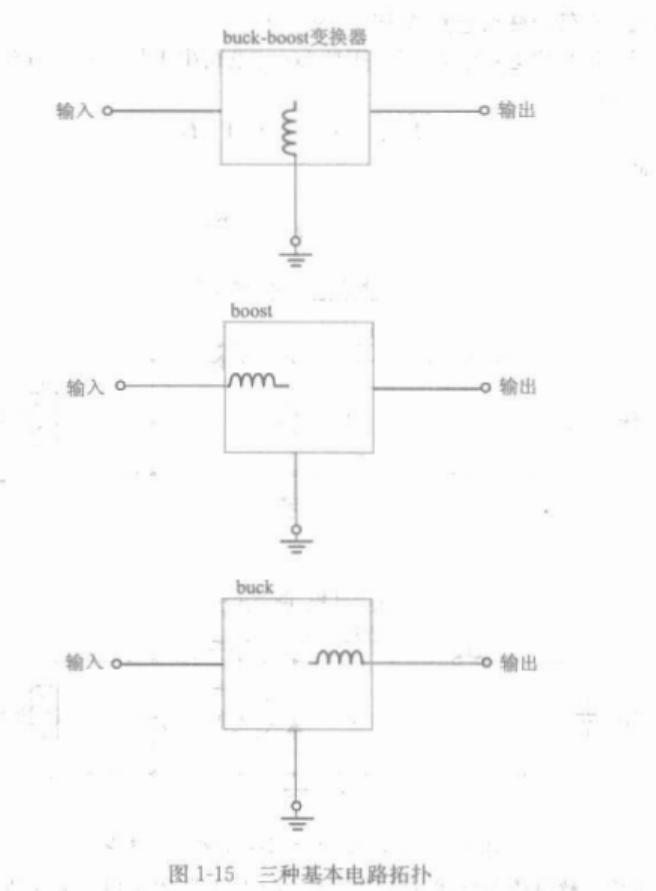
只有三种连接方式具有合适的地参考点,即电感连接到输入端、输出端、和公共地
1.4.10 升压拓扑

$$V_{\mathrm{O}}=V_{\mathrm{IN}}\times\frac{1}{1-D}\text{(升压 })$$
1.4.11 降压拓扑
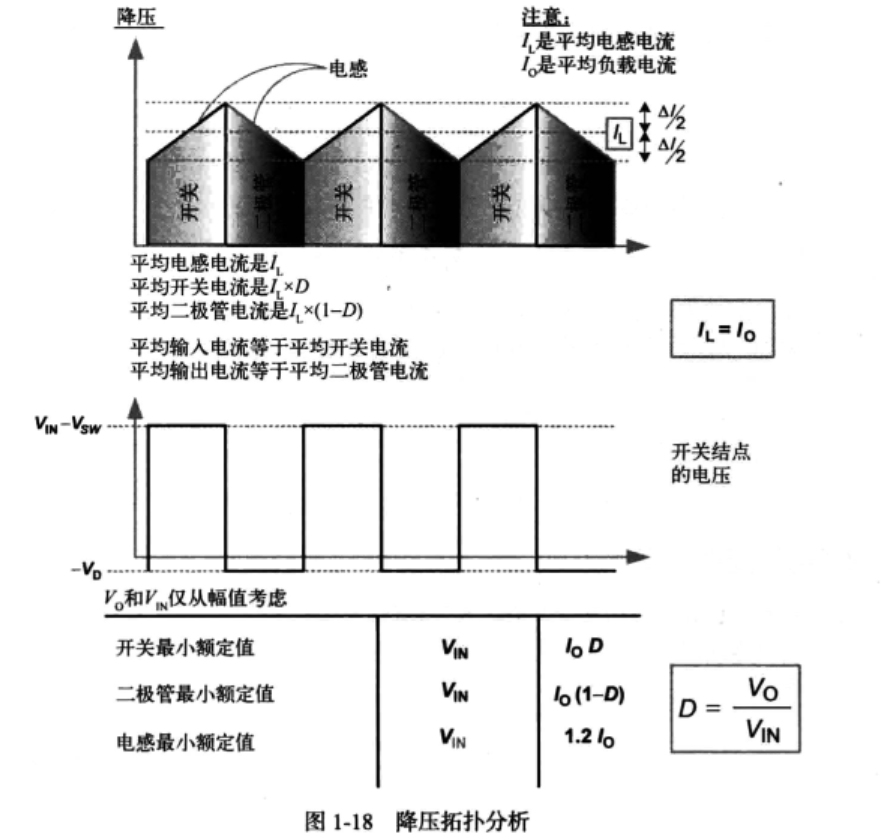
$$V_{\mathbf{O}}=V_{\mathbf{IN}}\times D\text{(降压 })$$


